過去の応用情報技術者の午後の試験で、循環小数の循環節を求めるのに「ウサギとカメのアルゴリズム」を使ったプログラミングの問題が出題されたことがあります。これが、ちょっと面白かったので分数と循環節についてまとめてみました。
循環小数の循環節を求める
まず、有理数は以下のように、ちょうど割り切れる有限小数というものと(例えば1/2=0.5、1/125=0.008)、ある桁以降から数字の並びが繰り返し続く無限小数というものに分けられます。(例えば、1/3=0.333333…(以下3が繰り返し続く)、1/7=0.14285714285742857…(以下142857が繰り返し続く))
今回の問題は、無限小数で繰り返し現れる数字の並び(循環節)が現れる初めの位置と、
循環説の終わりの位置を計算する問題です。(簡単のため分子は常に1とします)
例として、1/108(=0.00925925925...)を計算してみます。
まず、1を10倍して108で割った商(0)を小数第1位に
次にその余り(10)を10倍して108で割った商(0)を小数第2位に
次にその余り(100)を10倍して108で割った商(9)を小数第3位に
次にその余り(28)を10倍して108で割った商(2)を小数第4位に
と計算していきます。
0 ← 1を108で割った商 (余りは1)
0 ← 上の余り(1) を10倍した数(10)を108で割った商(0)、 (余りは10)
0 ← 上の余り(10) を10倍した数(100)を108で割った商(0) (余りは100) ☆
9 ← 上の余り(100) を10倍した数(1000)を108で割った商(9) (余りは28)
2 ← 上の余り(28) を10倍した数(280)を108で割った商(2) (余りは64)
5 ← 上の余り(64) を10倍した数(640)を108で割った商(5) (余りは100) ☆
9 ← 上の余り(100) を10倍した数(1000)を108で割った商(9) (余りは28)
2 ← 上の余り(28)を10倍した数(280)を108で割った商(2) (余りは64)
☆の行で余りが一致しています。これ以降、商の並びも同じになっています。
余りの値が、今までに計算した余りと一致すると、それ以降の商の値の並びが同じになり繰り返していることがわかります。
一般的に自然数nで割った余りは0~n-1までの整数値なので、割り切れる場合を除くと、割った余りが一致するまでのステップ数は、高々n-1回となります。つまり、循環節の長さはn-1より大きくなり得ません。
循環節を求めるには、今までの計算した余りの値をリストとして覚えておき、新しく計算した余りをリストの中の余りと比較して一致していれば循環節の初めの位置として計算できそうです。
Cのプログラムを作成してみました。
#include <stdio.h>
#include <stdlib.h>
// 分数 1 / n の循環節の位置を求める
void junkan(int n)
{
int m = 1; // 剰余を保持する変数(初期値1)
int s = 0; // 循環節の開始位置
int t = 0; // 循環節の終了位置
int* list = (int*)calloc(n - 1, sizeof(int)); // リストの初期化
while (true)
{
// mが剰余リストにある場合はループ終了
for(s = 0; list[s]; s++)
if(m == list[s])
goto END;
// 剰余リストになかった場合は、終端に追加
list[s] = m;
// 次の剰余を計算
m = (m * 10) % n;
// 割り切れる場合はループ終了
if (m == 0) goto END;
t++;
}
END:
free(list); // リストの解放
printf("n = %d, s = %d, t = %d\n", n, s + 1, t); // 結果を出力
}
int main()
{
junkan(108);
return 0;
}出力結果
n = 108, s = 3, t = 5
うまく計算できているようです。
この方法では計算した剰余の履歴を保存するために、入力値nに対してn-1個の整数リストが必要でした。
この方法に対して、「ウサギとカメのアルゴリズム」 という方法があります。
次項では、の方法についてまとめてみたいと思います。
ウサギとカメのアルゴリズム
前回、循環節を求める簡単なプログラムを紹介しましたが、この方法では入力値nに対してn-1個のリストを作る必要がありました。
今回は、リストが不要な「ウサギとカメのアルゴリズム」(フロイドの循環検出法)を紹介します。
この方法は、2つの変数(ウサギとカメ)を使います。ウサギとカメは1をnで割った剰余1をスタート地点とし、同時にスタートします。ウサギは1つ飛ばしで移動します。カメは1ずつ移動します。速さの違うウサギとカメがトラック上を走るような感じで、いずれウサギはカメに追いつき、ある位置でならびます。
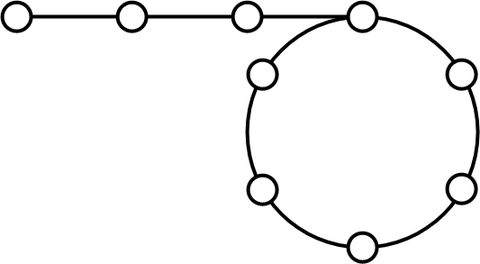
ここで、ウサギがうまくぶつからずにカメを追い抜いてしまうのではないかと思うかもしれませんが、その心配はありません。
もし、ウサギがカメを追い抜き、カメはi番目の位置、ウサギはi+1番目の位置にあるとすると、1つ前の状態ではウサギもカメもi-1番目の位置にいたことになります。
ウサギがカメに追いついた時点でウサギをスタート地点にワープさせ、今度はウサギも1ずつ移動させていきます。再びカメと並んだ位置がループの開始点となっています。次に、カメをループの開始点で待たせておき、ウサギを1個ずつ移動させます。再度、ウサギとカメが出会った時点がループの終了点となります。
なぜ、そうなっているかというと、、
ここで、出発点からループの開始点までの長さをK。ループの長さをLとします。
カメがスタート地点から出発して、ループの開始点に到達したとき、ウサギはカメの2倍、2K進んでいるはずです。
また、ウサギはループの開始点からはK進んでいます。
Kはループの長さLより大きいかもしれないので、ウサギのループ内の位置を剰余K’=K mod Lと表します。
このとき、カメはウサギのK’ステップ後ろにいます。逆にみて、ウサギはカメのL-K’ステップ後ろにいます。
1回のステップで、ウサギとカメは1ずつ近づくので、ウサギはカメにL-K’ステップで追いつきます。
追いついた時点で、ウサギをスタート地点にワープさせます。
ここで、カメはループの開始点からL-K’だけ移動した位置にいます。
ウサギとカメを1ずつ移動させていくと、ウサギとカメはループの開始点で出会うことになります。
なぜなら、ウサギがループの開始点までKステップで動く間に、カメはループ内の位置L-K’の位置からKステップ移動します。ループ内ではKステップ移動するとK’だけ進むので、カメはループのL-K’+K'=L=0地点つまりループの開始点に戻っているはずです。
最後に、カメをループの開始点で待たせ、ウサギを1個ずつ進ませ再びカメと出合う位置がループの終了点となります。
このアルゴリズムをC言語プログラムで記述すると以下のようになります。
#include <stdio.h>
void junkan2(int n)
{
int m = 1; // カメ。剰余を保持する変数(初期値1)
int p = 1; // ウサギ。剰余を保持する変数(初期値1)
int s = 0; // 循環節の開始位置
int t = 0; // 循環節の終了位置
if (n > 0)
{
// ウサギとカメが出合う地点を探す
while (true)
{
m = (m * 10) % n;
p = (p * 10) % n;
p = (p * 10) % n;
if (m == p)break;
}
// pが非ゼロ。割り切れない場合
if (p != 0)
{
// ウサギをスタート地点に戻し、再びカメと出合うまでループを回す
p = 1;
s = 1;
while (m != p)
{
s++;
m = (m * 10) % n;
p = (p * 10) % n;
}
// カメを止めて、ウサギだけ1ずつ進める
p = (p * 10) % n;
t = s;
while (m != p)
{
t++;
p = (p * 10) % n;
}
}
}
printf("n = %d, s = %d, t = %d\n", n, s, t); // 結果を出力
}
int main()
{
junkan2(108);
return 0;
}出力結果 n = 108, s = 3, t = 5
見事、前回のプログラムと比べてリストの確保が不必要になっています。